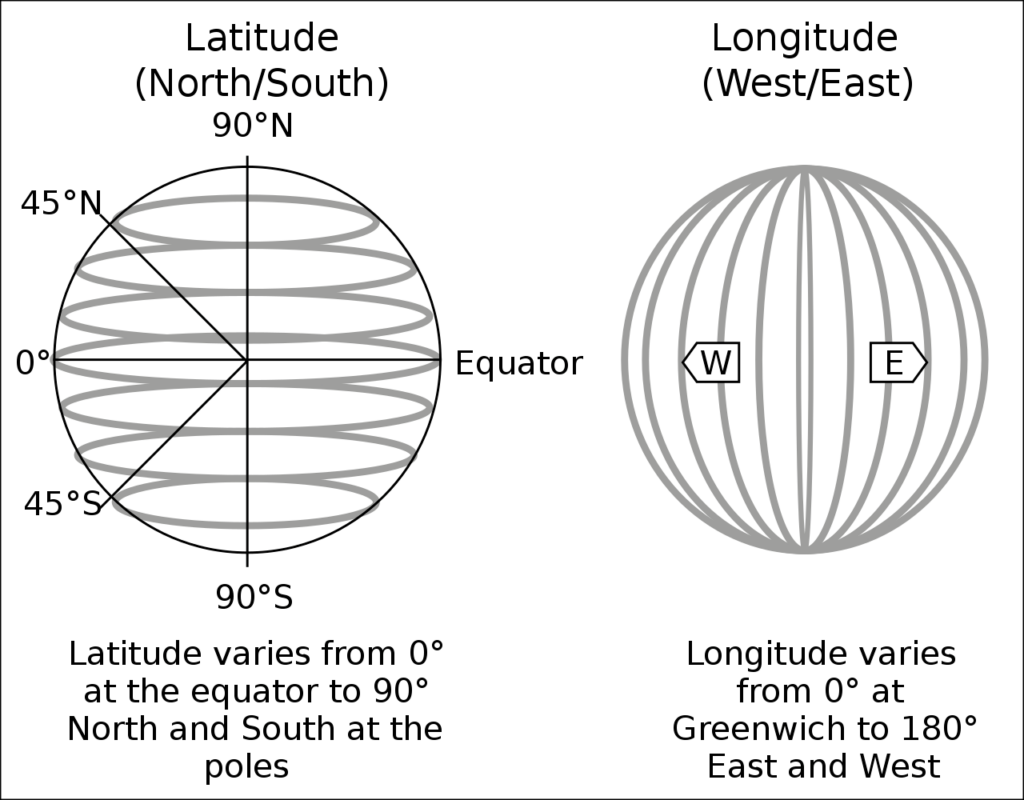
How to Convert Degrees Minutes Seconds to Decimal Degrees
First of all let’s take a look at the symbols:
° : degree
‘ : minute
“ : second
1 minute is equal to 60 seconds.
1 degree is equal to 1 hour, that is equal to 60 minutes or 3600 seconds.
To calculate decimal degrees, we use the DMS to decimal degree formula below:
Decimal Degrees = degrees + (minutes/60) + (seconds/3600)
DD = d + (min/60) + (sec/3600)
Latitude: 52.377956 DMS Lat: 52° 22' 40.6416'' N 52.0 22/60 ~= .3667 40/3600 ~= 0.01 Longitude: 4.897070 DMS Long: 4° 53' 49.4520'' E
(()=> {
const deg2rad = degrees => degrees * (Math.PI / 180);
const rad2deg = radians => radians * (180 / Math.PI);
const nm2km = nm => nm * 1.852;
const distance = (a, b) => {
if (a[0] == b[0] && a[1] == b[1])
return 0;
const radlat1 = deg2rad(a[0]);
const radlat2 = deg2rad(b[0]);
const radtheta = deg2rad(a[1] - b[1]); // diff East and West
let dist =
Math.sin(radlat1) * Math.sin(radlat2) + // diff North - South
Math.cos(radlat1) * Math.cos(radlat2) // diff North - South
* Math.cos(radtheta); // diff East and West
if (dist > 1) // overflow
dist = 1;
return rad2deg(Math.acos(dist)) * 60; // NM (nautical miles)
};
console.log(distance([30, 30], [60, 60])); // 2165.866861755054
console.log(nm2km(distance([30, 30], [60, 60]))); // 4011.18542797036
})();Reference: https://www.geodatasource.com/developers/javascript
const deg2rad = degrees => degrees * (Math.PI / 180);
const rad2deg = radians => radians * (180 / Math.PI);
interface ICoordinate {
latitude: number,
longitude: number
}
const distanceInKm = (a: ICoordinate, b: ICoordinate) => {
if ((a.latitude == b.latitude) && (a.longitude == b.longitude)) {
return 0;
} else {
const radlat1 = deg2rad(a.latitude);
const radlat2 = deg2rad(b.latitude);
const radtheta = deg2rad(a.longitude - b.longitude);
let dist =
Math.sin(radlat1) * Math.sin(radlat2) +
Math.cos(radlat1) * Math.cos(radlat2)
* Math.cos(radtheta);
if (dist > 1) {
dist = 1;
}
dist = rad2deg(Math.acos(dist));
dist = dist * 60 * 1.853159616;
return dist;
}
}
//distance the simple (but wrong) way
distanceSimple(a: ICoordinate, b: ICoordinate): number {
return Math.sqrt((a.latitude - b.latitude) * (a.latitude - b.latitude) +
(a.longitude - b.longitude) * (a.longitude - b.longitude));
} distanceInKm(a: ICoordinate, b: ICoordinate) {
if ((a.latitude === b.latitude) && (a.longitude === b.longitude)) {
return 0;
} else {
const radlat1 = deg2rad(a.latitude);
const radlat2 = deg2rad(b.latitude);
const radtheta = deg2rad(a.longitude - b.longitude);
let dist = Math.sin(radlat1) * Math.sin(radlat2) + Math.cos(radlat1) * Math.cos(radlat2) * Math.cos(radtheta);
if (dist > 1) {
dist = 1;
}
dist = rad2deg(Math.acos(dist));
dist = dist * 60 * 1.853159616;
return dist;
}
}https://www.movable-type.co.uk/scripts/latlong.html
const R = 6371e3; // metres
const φ1 = lat1 * Math.PI/180; // φ, λ in radians
const φ2 = lat2 * Math.PI/180;
const Δφ = (lat2-lat1) * Math.PI/180;
const Δλ = (lon2-lon1) * Math.PI/180;
const a = Math.sin(Δφ/2) * Math.sin(Δφ/2) +
Math.cos(φ1) * Math.cos(φ2) *
Math.sin(Δλ/2) * Math.sin(Δλ/2);
const c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
const d = R * c; // in metresFinding direction in degrees between two positions?
TODO!
Initial Bearing
const y = Math.sin(λ2-λ1) * Math.cos(φ2); const x = Math.cos(φ1)*Math.sin(φ2) - Math.sin(φ1)*Math.cos(φ2)*Math.cos(λ2-λ1); const θ = Math.atan2(y, x); const brng = (θ*180/Math.PI + 360) % 360; // in degrees
| JavaScript:(all angles in radians) | const y = Math.sin(λ2-λ1) * Math.cos(φ2); const x = Math.cos(φ1)*Math.sin(φ2) – Math.sin(φ1)*Math.cos(φ2)*Math.cos(λ2-λ1); const θ = Math.atan2(y, x); const brng = (θ*180/Math.PI + 360) % 360; // in degrees |
| Excel:(all angles in radians) | =ATAN2(COS(lat1)*SIN(lat2)-SIN(lat1)*COS(lat2)*COS(lon2-lon1), SIN(lon2-lon1)*COS(lat2)) *note that Excel reverses the arguments to ATAN2 – see notes below |
https://www.npmjs.com/package/geodesy
https://developers.google.com/public-data/docs/canonical/countries_csv
http://www.geonames.org/
http://download.geonames.org/export/dump/
168700cookie-checkDistance Lat-Long to Kilometers